逻辑斯蒂回归（Logistic_Regression）

《PyTorch深度学习实践》- 刘二大人p6

关于回归和分类

回归：对于前面的题来说，训练好后，输入x=4时，根据训练成果和构造的y_hat=w * x + b，即刻输出预测值y=8。但实际问题更为复杂，输出值很难为具体值。

分类：那经典的MNIST来说，这是一张充满0~9手写体的数据库，其中训练集6w，测试集1w。红圈处的7和9十分相似，这是y=7还是y=9呢？这是通过概率大小分类，从而认为y=或者是y=9。当p(p(y=7))=0.2，p(p(y=9))=0.8时，可以确认y=9。

逻辑回归（Logistic Regression）

Logistic Regression Function是一种用于解决二分类（0 or 1）问题的机器学习方法，用于估计某种事物的可能性。Logistic Regression Function 是Sigmoid Function中的一种，还有其他函数。

例子：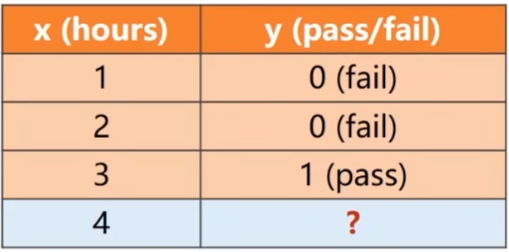

学习时间x，通过考试结果y。y只有fail（0）和pass（1）两类结果，其中p(y-hat=0)+p(y-hat=1)=1，故只需要计算出一个，另一个自然可得出。

现在x=1，x=2都不能通过，x=3通过了，那现在x=4可以通过吗？逻辑回归就是解决二分类的方法。

逻辑斯蒂函数（Logistic_Function）

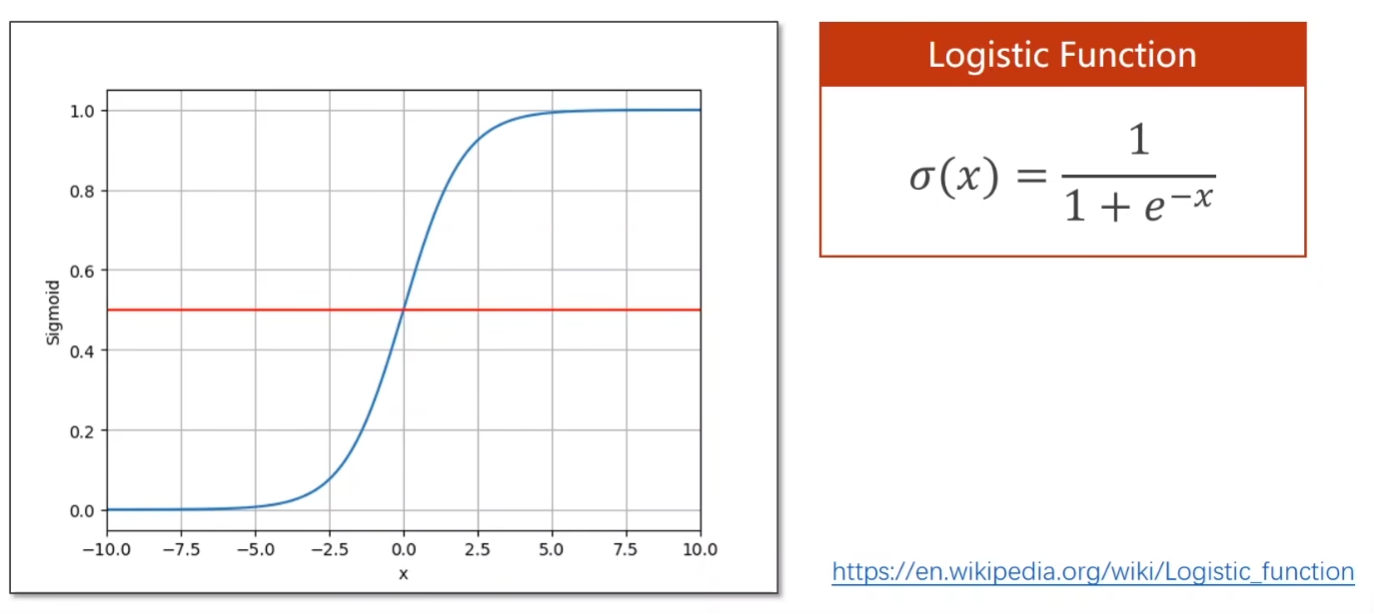
x - > + ∞，δ(x) - > 1

x = 0，δ(x) = 0.5

x - > - ∞，δ(x) - > 0

回到本题，y-hat取值为实数值，该如何将y-hat结果转化成概率呢？现引入逻辑斯蒂函数，因为输入x ∈ (-∞, +∞)，输出δ(x) ∈ [0, 1]，将x换成y-hat，即求δ(y-hat) = 1 / (1+e^-y-hat)。此时y-hat之前所取的实数值作为输入，输出[0, 1]，变为概率。如p(y-hat = 6) = 0.6 > 0.5 ，

模型和计算图前后对比

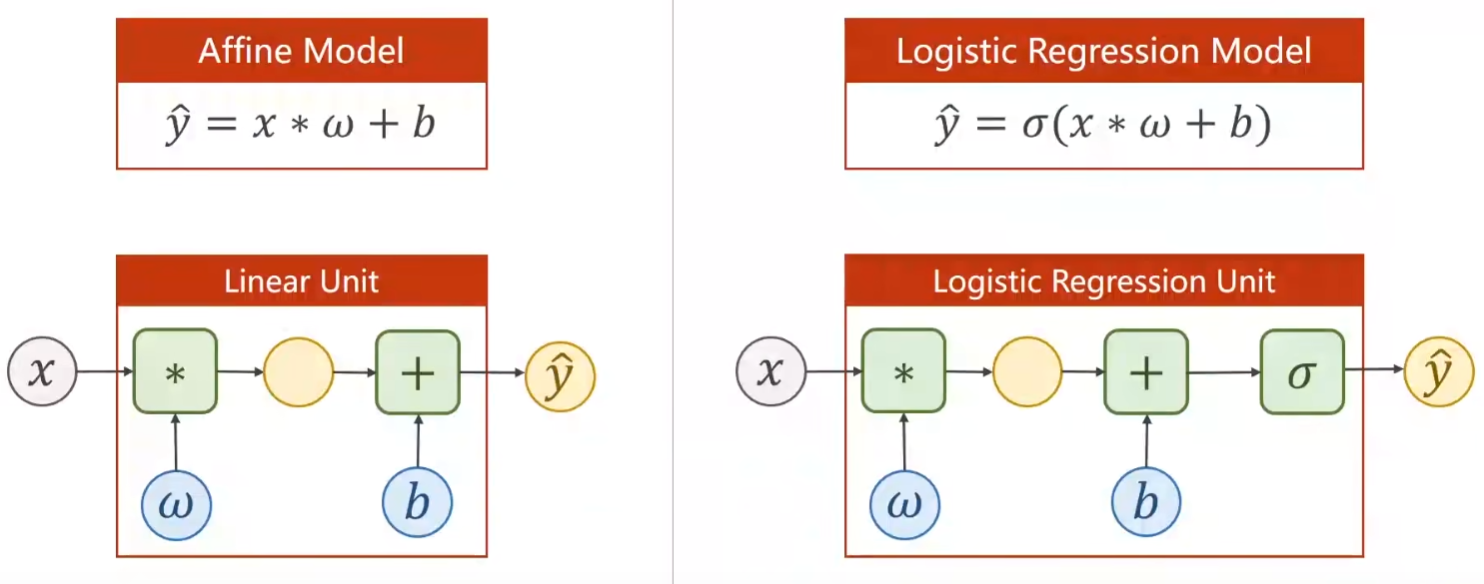
Loss 函数前后对比

y-hat已经从实数值变为概率。

y-hat = P(class = 1)

1 - y-hat = P(class = 0)

新函数称为BCE Loss，即从MSE Loss变为BCE Loss。

代码

import torch
import matplotlib.pyplot as plt
import  torch.nn.functional as F
import numpy as np

# Prepare dataset
x_data = torch.Tensor([[1.0],[2.0],[3.0]])
y_data = torch.Tensor([[0], [0], [1]])      #更新

# Design Model
class LogisticegressionModel(torch.nn.Module):    #更新
    def __init__(self):
        super(LogisticegressionModel, self).__init__()
        self.linear = torch.nn.Linear(1, 1)

    def forward(self, x):
        y_pred = F.sigmoid(self.linear(x))
        return  y_pred

model = LogisticegressionModel()

# Construct Loss and Optimizer
criterion = torch.nn.BCELoss(size_average=False)    # 更新
optimizer = torch.optim.SGD(model.parameters(), lr=0.01)


for epoch in range(1000):
    y_pred = model(x_data)
    loss = criterion(y_pred,y_data)
    print(epoch,loss.item())

    # # 画图用
    # epoch_list.append(epoch)
    # mse_list.append(loss.item())    #!弹幕提醒，加上.item()

    optimizer.zero_grad()
    loss.backward()
    optimizer.step()    # .step() 用来更新Updatae

print('w =',model.linear.weight.item())
print('b =',model.linear.bias.item())

# Output weight and bias
x_test = torch.Tensor([[4.0]])
y_test = model(x_test)
print('y_pred = ', y_test.data)


x = np.linspace(0, 10, 200)     # 0~10,采200个点
x_t = torch.Tensor(x).view(200, 1)	  # .view()等于numpy的.reshape()，变为200行一列的矩阵
y_t = model(x_t)
y = y_t.data.numpy()    # 使用.data.numpy()，拿到y_t中的数，且变为numpy的数组类型，而非张量
plt.plot(x, y)
plt.plot([0, 10], [0.5, 0.5], c = 'r')
plt.xlabel("Hours")
plt.ylabel("Probaability of Pass")
plt.grid()
plt.show()

结果图

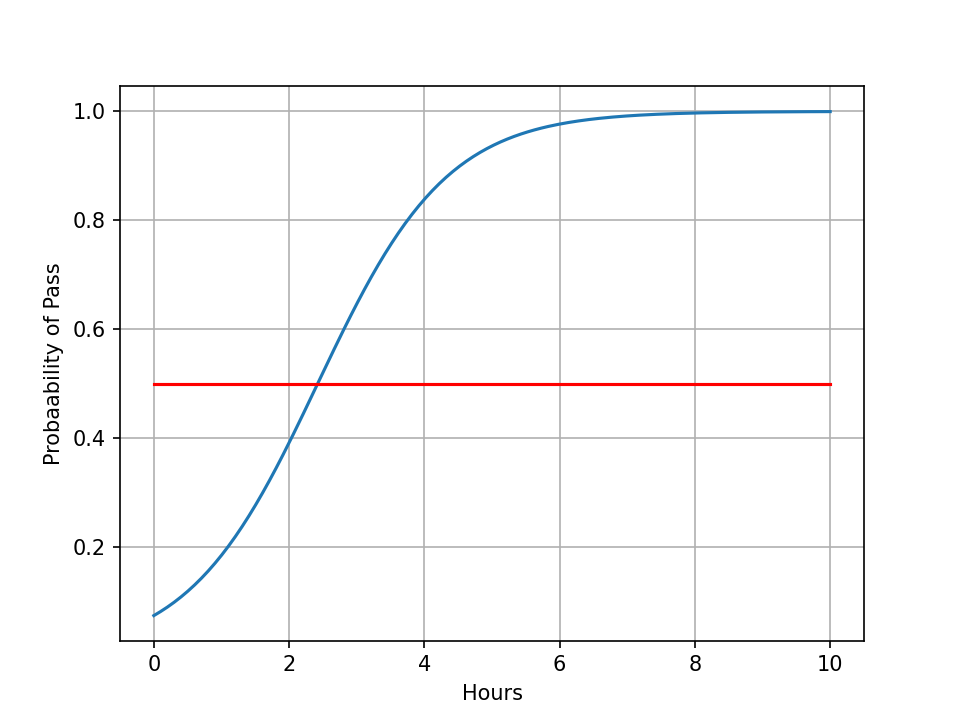
红线处为0.5，即通过率50%处。可见学习时间2.5时，通过率为50%。